Beer-Lambert’s Law Experiment
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 1151 words | ✅ Published: 30 Jan 2018 |
Aim
To learn and understand the basics and mathematical calculations of the following problem and write programs accordingly.
Problem 1: Suppose an outdoor multispectral image is captured by a camera with a path length of 1-3 microns. A part of the intensity is attenuated by the absorption of small particles in the atmosphere for that spectral range and let the scattering by the small particles for that spectral range is 0.
Find the total attenuation in the spectral range using Simpson 1/3 , trapezoidal and Euler integration methods and comment in your findings.
Scope/Application
Beer Lambert’s law relates the attenuation of light to the properties of the material through which the light is passing. When light passes through a medium some amount of light is absorbed by the medium. For this absorption intensity of light reduces.
Beer Lambert’s law states that the quantity of light absorbed is directly proportional to the concentration of the substance and the path length of the light through the transmission medium
Beer Lambert’s law is used to find total attenuation of light when light passes through a medium(considering scattering is zero).It is also used to find the concentration of medium in chemical analysis, medium length in some application and absorbance of medium when necessary.
Introduction of Beer Lambert Law
Lambert’s law is (Related to thickness/path length of medium)
When light passes through an absorbing medium its intensity decreases exponentially as the path length of the absorbing medium increases.
I = I0 e-k1 L ……………………………………….(i)
(where L is the length of medium and k1 is molar extinction/absorption co-efficient for the absorbing material)
Beer’s law is (Related to concentration of absorbing medium)
When light passes through medium(absorbing) its intensity decreases exponentially as the concentration of the absorbing medium increases.
I = I0e-k2C …………………………………..(ii)
(C concentration of medium and k2 is absorption co-efficient for the absorbing material)
Combining both Beer’s and Lambert’s law we get
I = I0 e-k3CL combining eqn (i) and (ii)
Where I0 = Incident light intensity
I = Transmitted Light intensity
C=concentration / volume
L= path length of medium
We consider an outdoor multispectral image is captured by a camera with a spectral range of 1-3 microns. A part of the intensity is attenuated by the absorption of small particles in the medium.so image will be attenuated. Beer Lambert’s law find the attenuation caused by absorption for that spectral range and let the scattering by the small particles for that spectral range is 0.
Objectives
In a given path length 1 to 3 micron, we have considered a constant value of molar extinction/absorption co-efficient.and now we need to find the absorbance & total attenuation of the incident light using Beer’s Lambert Law. And then applying Simpson’s 1/3, Trapezoidal and Euler Integration in it compare the result.
System flow
Implementation of the Beer Lambert’s law needs a proper mathematical understanding of the Beer Lambert’s law. Here I am showing how to set the equation using its mathematical basics
First we apply Beer Lambert’s Law for a medium which absorbs light in spectral range 1-3 micron. Considering no scattering we assume I0 is the incident light to the medium Air of attenuation coefficient 1.64at temperature 20oC. Here path length travelled by light is 1 to 3 micron.
According to Beer Lambert’s law light intensity is decreased if concentration & path length increase.
So we get the equation I=Io e-kcl = Io e-µl
Now as we know the path length l and attenuation coefficient µ, we calculate absorbance of the medium using eqn
Log10  = kcl (Where l is constant)
= kcl (Where l is constant)
 = e kcl
= e kcl
But now for a spectral range 1 to 3 micron path length we need to formulate a new equation by integrating ranged from .001mm to .003 mm

 [Here x is path length and c is attenuation coefficient]
[Here x is path length and c is attenuation coefficient]
Solving the above eqn we get total absorbance. Thus Beer Lambert’s law is successfully implemented in our problem.
Now we apply Simpson 1/3 rd, trapezoidal rule on Beer’s Lambert Law to find total attenuation.
Finally compare the result of Simpson’s 1/3 rd and Trapezoidal rule with the actual integration.
 Flow Diagram:
Flow Diagram:

















Math
Beer-Lambert Law Concept
Consider a light incident on a medium with area A and thickness dx and concentration of molecules C. Number of molecules illuminated by light of incident intensity Ix is CAdx.
Total effective area σCAdx. Probability of light being absorbed in thickness dx is
 =
=  dx [where dIx is the change in intensity across dx and σ is scattering coefficient]
dx [where dIx is the change in intensity across dx and σ is scattering coefficient]
So we can write,
 =
=  dx ………… (i)
dx ………… (i)
Now we integrate both sides of (i)

ln (I) – ln(I0) = ln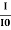 = – σCx
= – σCx
I = I0e-σCx = I0 e–µx ……………….(ii)
The co-efficient µ=σ C is the linear attenuation co-efficient. Here C=Absorbing co-efficient & σ = Scattering co-efficient.
The ibrightness of light decreases exponentially with depth in the medium.
So we can tell Beer-Lambert Law is also a function of( λ), i.e.
I (λ) = I0 (λ) e-µ(λ)x………………………(iii)
Calculation
(Here we considered linear attenuation)
Given spectral range 0.001 mm to 0.003 mm
Let we consider Absorbing coefficient(C) of Transmission Medium (Air) = 1.64 at 20o C. So total absorption (A) of light is calculated by integrating in the spectral range,
 [from eqn ii]
[from eqn ii]
= ———– (1)
———– (1)
= 
= 0.002006571
Now we can easily calculate attenuated intensity of light (I).
Attenuation is the loss of light intensity over distance. The greater the distance, the lower is the intensity
Where I=I0 -Attenuation
Trapezoidal rule
We know, in case of multiple application of Trapezoidal rule, the formula is:
 =
=  [f(x0) + 2
[f(x0) + 2 ) + f(xn)]
) + f(xn)]
So, here applying the above formula for equation (1) we get:
 = 0.0005[[
= 0.0005[[ 0.001 + 2
0.001 + 2 + [
+ [ ] 0.003]
] 0.003]
= 0.0005[1.001641346 + 2.00657077 + 1.004932123]
= 0.0005[4.013144239]
=0.002006572 (Ans.)
Here,
x0 = x0.001, xn = x0.003, b = 0.003, a = 0.001, n = 2,  = 0.0005.
= 0.0005.
Simpson’s  rule:
rule:
We know, composite Simpson’s rule formula is written as:
 =
=  [f(x0) + 4
[f(x0) + 4 ) +2
) +2 ) + f(xn)]
) + f(xn)]
So, here applying the above formula for equation (1) we get:
 = 0.0003[[
= 0.0003[[ 0.001 + 4
0.001 + 4 + [
+ [ ] 0.003]
] 0.003]
= 0.0003[1.001641346 + 4.01314154 + 1.004932123]
= 0.001805914 (Ans.)
Here,  = 0.0003.
= 0.0003.
Euler’s formula
Here,  =
= 
y(0.001) =  = 0 (assumption)
= 0 (assumption)
y(0.003) =  ≈
≈ 
and we have to find the value of equation (1) using Euler’s formula which is,
 =
=  + f (
+ f ( ,
,  ) h
) h
let us choose h = 0.001
Step-1
i=0,  = 0.001,
= 0.001,  = 0, h = 0.001
= 0, h = 0.001
 =
=  + f (
+ f ( ,
,  ) h
) h
= 0 + f (0.001, 0) 0.001
= 0.001001641
Step-2
i=1,  = 0.002,
= 0.002,  = 0.001001641, h = 0.001
= 0.001001641, h = 0.001
 =
=  + f (
+ f ( ,
,  ) h
) h
= 0.001001641 + f (0.001, 0.001001641) 0.001
= 0.0020049426
This  is actually the value of the function at
is actually the value of the function at  i.e. at (
i.e. at ( +h) or (0.002+0.001) or 0.003.
+h) or (0.002+0.001) or 0.003.
So,
 =
= 
= 0.0020049426-0
= 0.0020049426 (Ans.)
We find that the result of all above technique is almost same if we take approximation i.e.0.002.
CODES and OUTPUT:
Beer Lambert’s Law
#include
#include
#include
int main()
{float absorbtion,m,l,u;
printf(“nEnter spectral range”);
scanf(“%f%f”,&l,&u);
printf(“nnenter the value of absorption cofficient”);
scanf(“%f”,&m);
absorbtion=(1/m)*(pow(2.718,(m*u))-pow(2.718,(m*l)));
printf(“nnTotal absorption is %f: “,absorbtion);
getch();
}
Output

Simpson 1/3rd rule
#include
#include
#include
void main()
{float x[10],y[10],Total=0,h,t;
int i,n,j,k=0;
printf(“nhow many values you will enter: “);
scanf(“%d”,&n);
for(i=0; i
{ printf(“nn x%d: “,i);
scanf(“%f”,&x[i]);
printf(“nn f(x%d): “,i);
scanf(“%f”,&y[i]); }
h=x[1]-x[0];
n=n-1;
Total = Total + y[0];
for(i=1;i
{ if(k==0) { Total = Total + 4 * y[i];
k=1 }
else { Total = Total + 2 * y[i];
k=0; } }
Total = Total + y[i];
Total = Total * (h/3);
printf(“nn I = %f “, Total);
getch();}

Trapezoidal rule
#include
#include
#include
int main(){
float x[10],y[10], Total =0,h;
int i,n,j,k=0;
float fact(int);
printf(“nhow many values of ranges you will be enter: “);
scanf(“%d”,&n);
for(i=0; i
{printf(“nn x%d: “,i);
scanf(“%f”,&x[i]);
printf(“nn f(x%d): “,i);
scanf(“%f”,&y[i]); }
h=x[1]-x[0];
n=n-1;
for(i=0;i
if(k==0) { Total = Total + y[i];
k=1; }else
Total = Total + 2 * y[i];}
Total = Total + y[i];
Total = Total * (h/2);
printf(“nn I = %f “, Total);
getch();}

Future Work & Scope
This Beer Lambert’s law can be used in image processing application where atmospheric condition is poor to find the attenuation of light and image by absorption of light.
Implementing Euler Method.
References
- Weisstein, Eric W. “Simpson’s Rule.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/SimpsonsRule.html. (Accessed on 26.04.2015)
- Basics of Trapezoidal and Simpson Rules, www.math.umd.edu/~jmr/141/Simpson.pdf.
- Lal, A. K., Simpson’s Rule, 2007, http://numericalmethods.eng.usf.edu.(Accessed on 20.04.2015)
- http://numericalmethods.eng.usf.edu. (Accessed on 19.03.2015)
- Garrett, P., Absorption and Transmission of light and the Beer-Lambert Law, Lecture 21, 2006, www.physics.uoguelph.ca/~pgarrett/Teaching.html. (Accessed on 26.04.2015)
- Mudakavi, J. R., Modern Instrumental Methods of Analysis, Lecture – 07, Ultraviolet and Visible Spectrophotometry – 3 Theoretical Aspects, http://nptel.ac.in/courses/103108100/7 (Accessed on 26.04.2015).
- www.chemwiki.ucdavis.edu. (Accessed on 19.03.2015)
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal



